ブログ・お知らせ
【算数と数学】扉の奥の扉(灘中入試2日目より)
- 06_受験関連,算数・数学,08_東京大学
2020年の灘中学校の入試問題、二日目にもチャレンジしました。
(一日目については 「【算数と数学】万年カレンダー」をどうぞ)
解法が思いついても、その先にもう一段階あるような問題が多く、
受験生にとっては厳しかっただろうな、と思いました。
例えば1問目の(1)。
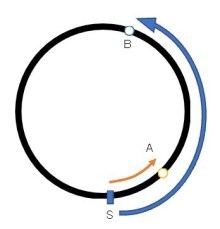
「600mの円形の散歩コースをA君は50m/分、B君は100m/分で同じ方向に進みます。
コースに沿って、スタート地点とA君の距離(A)、
スタート地点とB君の距離(B)、A君とB君の距離(C)を測り、
その中で一番短いものを「最短距離」(D)と呼びます。」(2020年灘中学入試問題より)
時間と「最短距離」(D)のグラフを描くのですが、
解法としては、(A)(B)(C)の3つのグラフを重ねて描いて、
その一番低いところを結んでいけば良いだけです。
(A)(B)のグラフは簡単に描けるのですが、問題は(C)。
既に(A)(B)のグラフが描けているだけに、
(A)と(B)の差をとれば良いように感じてしまいます。
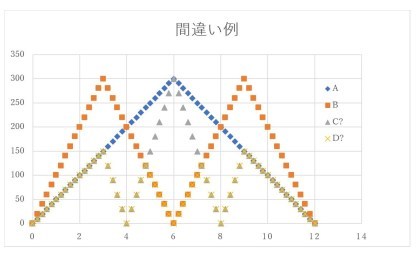
この考えで描いたのがこのグラフです。
しかし、これは間違い。
このコースは円形なので、300mの差がついた段階からは、反対側の長さを考えないといけません。
単純なことなので、愚直に解けば問題ないはずなのですが、
グラフの方に意識を取られると、足元をすくわれてしまいます。
また、第2問の(1)。
「A,B,C,D,Eの5桁の数があり、EはA+B+C+Dの下一桁です。
このうちの一つを書き換えた数字は28973でした。
元の数字として考えられる5桁の数をすべて書きなさい。」
この問題、最後の一桁は、それまでの4桁の数の合計「26」の下一桁「6」になるはず。
つまり「28976」がまず考えられます。
次に、「3」は変えていないのだとすると、「〇8973」「2〇973」「28〇73」「289〇3」。
上4桁の合計は「26」でしたから、これが「23」になるようにすれば良い、
のですが、これで解いたつもりになると、罠にはまる仕掛けです(笑)
(2)は、ここまで出来ていれば答えられるので、むしろサービス問題ですが、
(1)の「すべて」は怖い問題だなぁ、と思います。
つまり、合計「33」になるケースも考えなければならないのです。
どちらも、解法が思いついて、計算して、よし解けた!となった後に、抜け・落ちがないか確認が必要ですし、解法を思いついた段階で、別のケースも想定する必要のある問題です。
単に計算が出来る、解法が思いつく、のレベルではなく、
抜けのない解法を考えられることが要求されているわけで、
さすがの問題ですね。
前回も書きましたが、今、あるいは今回、この問題が解けなかったとしても、この問題にチャレンジする、チャレンジできるステージにいるということが素晴らしいのです。
受験した全ての小学生の皆さんに、輝かしい未来が待っていることを信じています!
- 計算ミス,計算問題,合格,算数,志望校,自分との戦い,数学,灘中,未来
オススメ記事
-
- お知らせ
-
- お知らせ
-
- お知らせ